NELSON PROVAZILEThe worst crises, the worst accidents, the worst natural and human disasters cause the most surprise. It seems that the more intense the event—from a devastating tsunami to a World War—the more unpredictable and uncontrollable it is. However, the French physicist and economist Didier Sornette, of the Swiss Federal Institute of Technology Zurich (ETH), believes otherwise. After two decades of comparing the frequency and intensity of extreme events in areas as different as economics and geology, Sornette is convinced that, although society and nature are too complex to allow us to predict many extreme events, the worst of these, called dragon kings, have unique characteristics that would allow us to anticipate and avoid them. In a talk at the TED Global conference held in June, 2013 in Edinburgh, Scotland, Sornette claimed that applying the dragon king theory to financial market regulation could prevent economic crises like the one that began in 2007 and caused hundreds of billions of dollars in losses in the U.S. stock markets. By 2008, global gross domestic product losses had reach $5 trillion.
Although his theory is not accepted by most economists, his ideas have been adopted by researchers in other areas who have already discovered evidence of dragon king-like events and the signals that precede them in the natural sciences, medicine and engineering. The most conclusive evidence observed so far was published late last year. An international team of physicists, led by researchers at the Federal University of Paraíba (UFPB) and including Sornette, were able to generate, observe, predict and eliminate dragon kings in fully controlled laboratory experiments for the first time.
In the state of Paraíba, the Brazilian researchers built a device capable of generating chaotic electrical oscillations and developed techniques that allowed them to manipulate these oscillations. They expect strategies similar to those used in the experiment will be useful in the control of extreme events in general. “We developed an electronic system, which was relatively easy to build, in order to test Sornette’s hypothesis experimentally,” explains physicist Hugo Cavalcante, of UFPB, first author of the study published in November 2013 in Physical Review Letters. The second author of the article, the physicist Marcos Oriá, from the same university, adds that the result “shows the possibility of identifying and anticipating extreme situations in complex systems, such as the financial market or the global climate.”
A specialist in optics and atomic physics, Oriá had long been interested in situations in which a relatively simple laser device generated chaotic behavior similar to that of more complex systems such as financial markets. However, Oriá only began to study the phenomenon after Cavalcante arrived at UFPB in 2011. Cavalcante spent three and a half years at Duke University, working in the lab of physicist Daniel Gauthier, who was well-known in the 1990s for the study of the synchronization of chaotic systems.
In order to study chaotic phenomena, Gauthier designed simple electronic circuits, the size of credit cards, in which he could vary both electrical current and voltage in a random, unpredictable way. The behavior of these electronic oscillators is described by simple, well-defined mathematical equations, but the oscillations are extremely sensitive to small changes. For this reason, a small electronic interference when the oscillator is set in motion can completely change its subsequent behavior. In practice, this characteristic makes it impossible to obtain precise predictions of current and voltage values after the start of the experiment. Nevertheless, Gauthier discovered how to connect two of these oscillators so that one of them, the master, oscillates freely and chaotically, while the other, the slave, follows the master in a synchronous manner.
Chaotic synchrony
Depending on how the master and slave oscillators were activated, however, the synchrony between them could disappear momentarily, then resume, in a series of brief random events that Gauthier called bubbling. Gauthier, Cavalcante and Oriá noted that, in most of these desynchronization events, the difference between the currents and voltages of the two oscillators was small. However, they also noted that, in a very few cases, this difference increased greatly.
They then sought a relationship between the number of bubbles (frequency) and their magnitude. They concluded that, in most cases, the frequency was proportional to the magnitude raised to an exponent whose value was the same for all events. This mathematical relationship is known as a power law. In a plot specially designed to accommodate numbers of several orders of magnitude, a power law takes the form of a simple straight line (see figure above).
No matter where they look, whether in nature or in society, physicists tend to encounter oscillatory phenomena with frequencies and magnitudes that obey power laws. The situations range from fluctuating stock prices to earthquakes or the propagation of electrical signals in the human brain. The similarities in phenomena that occur in such different situations have led researchers to call these “complex systems.” Each of these phenomena have a large number of components—take, for example, the agents in a market buying and selling stock or the neurons in the brain creating synapses—and act in a very characteristic way: the parts interact in an almost random way, but the sum of these interactions can generate surprising regularities, such as power laws.
And the fact that a phenomenon follows a power law could mean many things. This is because, according to this law, all manifestations of a phenomenon—in the case of the experiment in Paraíba, the voltage and current oscillations—are caused by the same underlying principle. This means, for example, that the origins of a large earthquake are, qualitatively, the same as those of a small seismic oscillation. The only distinction between the two events are their magnitudes or sizes. “Since we do not know in advance whether the magnitude of an event will be large or small,” explains Oriá, “the idea that all complex systems are inherently unpredictable has spread.”
Physicists who have applied this idea to the study of financial markets—founding a discipline known as econophysics—have concluded that large fluctuations in prices need not necessarily be caused by a major political or economic change. Often, a financial crisis can begin as a normal price fluctuation that, by chance, then increases to great proportions. Financial crises, therefore, would be inevitable given this reasoning. “This is a particularly pessimistic view and even dangerous, as it promotes an attitude of irresponsibility,” says Sornette, who has been warning his fellow physicists since the 1990s that not all financial fluctuations follow power laws, especially the larger ones.
What Sornette has claimed in the case of financial markets, Gauthier and his two Brazilian colleagues have observed with chaotic oscillators. In general, the desynchronization actually followed a power law. However, the most extreme events did not, and occurred at a much higher frequency. A plot of these events results in a prominent peak at one end of the graph, for which the researchers had no explanation.
Outliers
However, Gauthier, Cavalcante and Oriá soon noticed that the extreme desynchronization events were perfectly described by what Sornette called dragon kings. These are the most extreme events that can occur in a complex system and that occur at a frequency much greater than that expected based on the power law, which governs other system events.
The idea that the appearance of dragon kings is more predictable and controllable than other extreme events originated with the first successful application of Sornette’s theory, namely the prevention of the rupture of the fuselages of the Ariane rocket used by the European Space Agency. During the launches, engineers used acoustic sensors to record noise variations caused by stress in the structure of the rockets. When analyzing this data, Sornette realized that the noise corresponding to rupture represented dragon kings on his graphs. Based on this, he and his colleagues discovered how to detect the initial signs of the development of these ruptures in the acoustic emissions of the rockets and how to use them to prevent accidents.
Then, Sornette adapted his method—used even today during rocket launches—to monitor the economy, looking for warning signs of bursting financial bubbles. For the last five years he has been coordinating the ETH Financial Crisis Observatory, a project that monitors the prices of thousands of stocks sold on various stock exchanges, including the Brazilian stock exchange Bovespa. A bubble always begins in an optimistic atmosphere, in which traded assets are overvalued. Sornette believes that the best way to predict the arrival of a bubble is to look for signs that prices and other financial market indexes are going through what he calls super-exponential growth. This is when, for example, an investment yields 10% in one month, yields double the following month (20%) and double again (40%) two months later. Although it seems obvious that this growth cannot last forever, in the heat of trading investors tend to behave like a herd: eager to profit from the opportunities everyone around them seems to be enjoying, sometimes even the most cautious get carried away by the euphoria. At some point, however, when the artificiality of the situation becomes unsupportable, prices plummet, leading to a cascade of devaluation throughout the economy.
In his observatory, Sornette and his team detect super-exponential growth in the indices monitored and analyze their evolution. The objective is to obtain information to allow them to predict the critical moment when growth is replaced by a new regime—a drop or stagnation. Sornette affirms that he can detect the emergence of bubbles of varying sizes and is able to estimate when they are most likely to burst. An example is the Chinese economic miracle bubble, in which the country’s stocks grew 300% in a few years. In September 2007, during a conference for investors, Sornette warned that a regime change was about to occur. Almost no one listened, trusting that the Chinese government would do everything possible to maintain growth due to the preparations for the Beijing Olympics, which took place the following year. Three weeks after the conference, the Chinese market began to plummet, losing 70% of its value by the end of 2007.
Indeed, the frequency and magnitude of changes in global markets over the past 30 years have behaved according to a power law, with some extreme outliers representing the worst financial crises of the period, such as “Black Monday” in 1987, when the Dow Jones index depreciated $500 billion in a single day, and the global recession of 2007 and 2008, triggered by a crisis in the US housing market. According to Sornette, these crises are dragon kings, caused by a series of policies facilitating excessive credit expansion by central banks around the world, which reinforce super-exponential growth and other mechanisms that can lead to dragon kings.
JONATHAN UTZ / AFPPanicked: observers accompanying fall of stock prices on the Hong Kong stock exchange during the 1997 crisisJONATHAN UTZ / AFP
Strange attractors
In addition to super-exponential growth, Sornette explains that he has already identified three other dynamic mechanisms contributing to the formation of dragon kings. One is the bubbling phenomenon observed in detail for the first time in the pair of oscillators built by Cavalcante and Oriá.
The researchers relied on a theoretical model developed by physicist Edward Ott, of the University of Maryland, another expert on the chaotic behavior of electronic systems, to understand how dragon kings form in oscillators and what exactly was causing these desynchronization events to grow far more than other events.
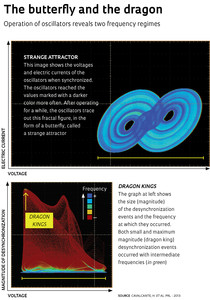
From previous work by Gauthier and Ott, the researchers already knew that a plot of the chaotic oscillations of these electronic circuits in an abstract space where the width, height and length represent properties that characterize the pair of oscillators at some moment traces out an infinite figure known as a strange attractor.
When in sync, the chaotic oscillations of the two circuits, although erratic, remain restricted to the lines of the strange attractor, whose shape resembles a pair of butterfly wings. “We found, however, that there is a specific point in the attractor with an instability so strong that it dominates the dynamics of the system,” explains Cavalcante.
This point of strong instability, located at the junction of the butterfly wings, is responsible for all desynchronization events. The more the circuit oscillation values approach that point, the greater the chance the trajectory describing the system will momentarily jump out of the plane of the attractor. The greater the jump, the greater the desynchronization between the oscillators. Most approaches to the point of instability cause the desynchronizations described by a power law. However, in special circumstances, when the trajectory comes too close to the unstable point, electronic noise and small differences between the circuit components can become amplified to the extent that they generate dragon kings.
“The difference between events following the power law and dragon kings is complicated, and we are still trying to understand the details,” says Cavalcante. Despite this, a qualitative understanding of the difference between the two types of desynchronizations has already allowed the researchers to identify specific combinations of oscillator voltages and currents that serve as an alarm indicating potential dragon kings. In tests at UFPB, when this variable reached a threshold value, signaling a dragon king was about to form, the researchers intervened slightly in the electronics of the oscillator system. As a result, they were able to keep the system trajectory within the attractor plane, preventing extreme desynchronization. The dragon kings disappeared completely (see graphs on page 46). “This small intervention was applied during only 1.5% of the total oscillator operating time, and it was 100% effective,” says Cavalcante.
Dragon eggs
Although the success of the experiment is exciting, the researchers understand the gigantic distance between the complexity of one pair of electronic oscillators and a financial market. “Applying this procedure to real systems is not trivial,” says economist Daniel Cajueiro, of the University of Brasília, who has experience in applying physics models to economics and has already worked with the Brazilian Central Bank. For now, he says, “this study can be taken as a starting point for a new line of research.”
The researchers hope that financial markets behave, at least under certain circumstances, like a system of interconnected chaotic oscillators. The oscillators, in this case, would be the market agents, buying and selling. Their decisions would be linked through herd behavior. In this scenario, a crisis could be avoided by identifying the points of instability in the system’s strange attractor and creating market rules that prevent the system from passing near them.
“I work with forecasts and I know how difficult it is to make them,” says economist Pedro Valls, director of the Center for Qualitative Studies in Economics and Finance of the Getúlio Vargas Foundation in São Paulo. “Believing in regularities is believing in determinism, which makes no sense in economics, statistics and finance.”
Valls thinks it is unlikely that the economy follows deterministic laws. According to him, in fact, the opposite is true: most of the econometric models used by researchers, governments and investors are stochastic, i.e., based on probabilities determined by random processes. Sornette counters that stochastic models can also result in dragon kings and that the best method for forecasting financial bubbles would be a hybrid model with deterministic and stochastic components. The problem, according to Sornette, is that many economists persist in believing that the mathematical solutions of their models should apply all the time. However, Sornette’s models apply only in certain critical moments, when the system becomes momentarily deterministic and predictable. Valls notes, though, that Sornette’s models are not the only ones capable of doing this: there is a vast econometrics literature discussing stochastic models capable of incorporating deterministic or stochastic changes. These models, called Markov switching models, can have different regimes, one of which could describe a crisis. These models allow us to quantify the probabilities of the market entering and exiting a crisis regime, thus helping predict bubbles.
While Cajueiro believes that Sornette’s theory has many merits, he notes at least two difficulties in making control of these complex systems feasible. The first is that, unlike Cavalcante and Oriá’s experiment, in which the statistics of extreme events was determined by collecting millions of data points, financial crises are not so frequent. “In this case, one would need to build a model for the system in an abnormal state and use a small sample of events,” explains Cajueiro.
And even if a model inspires enough confidence to be adopted, for example, by the Brazilian Central Bank to regulate the market, it might be simply impossible to implement the suggested interventions for practical or even ethical reasons. “Little is known about the response of economic agents to an intervention and what would happen if these agents anticipated the Central Bank’s response,” says Cajueiro. Since the financial market is not an isolated system, a change made to prevent the formation of a bubble could have unintended consequences with respect to variables such as inflation, exchange rates and unemployment.
Furthermore, Sornette himself recognizes that financial bubbles have a positive side. When driven by real increases in productivity, a result of the discovery of new sources of resources or promising technological innovations, they foster a climate of optimism that spreads to many economic activities, leading society to take risks and achieve successes that would be impossible otherwise.
The UFPB model could help in the testing of more realistic intervention methods that take into account the fascination with bubbles and the resistance of society to interrupting their growth until their collapse. “What we have done with the oscillators up to now was to use an optimal control method, which kills dragon kings when they are still eggs, before they hatch and grow,” explains Sornette. “We can use this system to study other, more limited interventions later in time in order to quantify the costs and consequences of our actions.”
Scientific article
CAVALCANTE, H.L.D.S. et al. Predictability and suppression of extreme events in a chaotic system. Physical Review Letters. V. 111, No. 19. Nov. 4, 2013.
