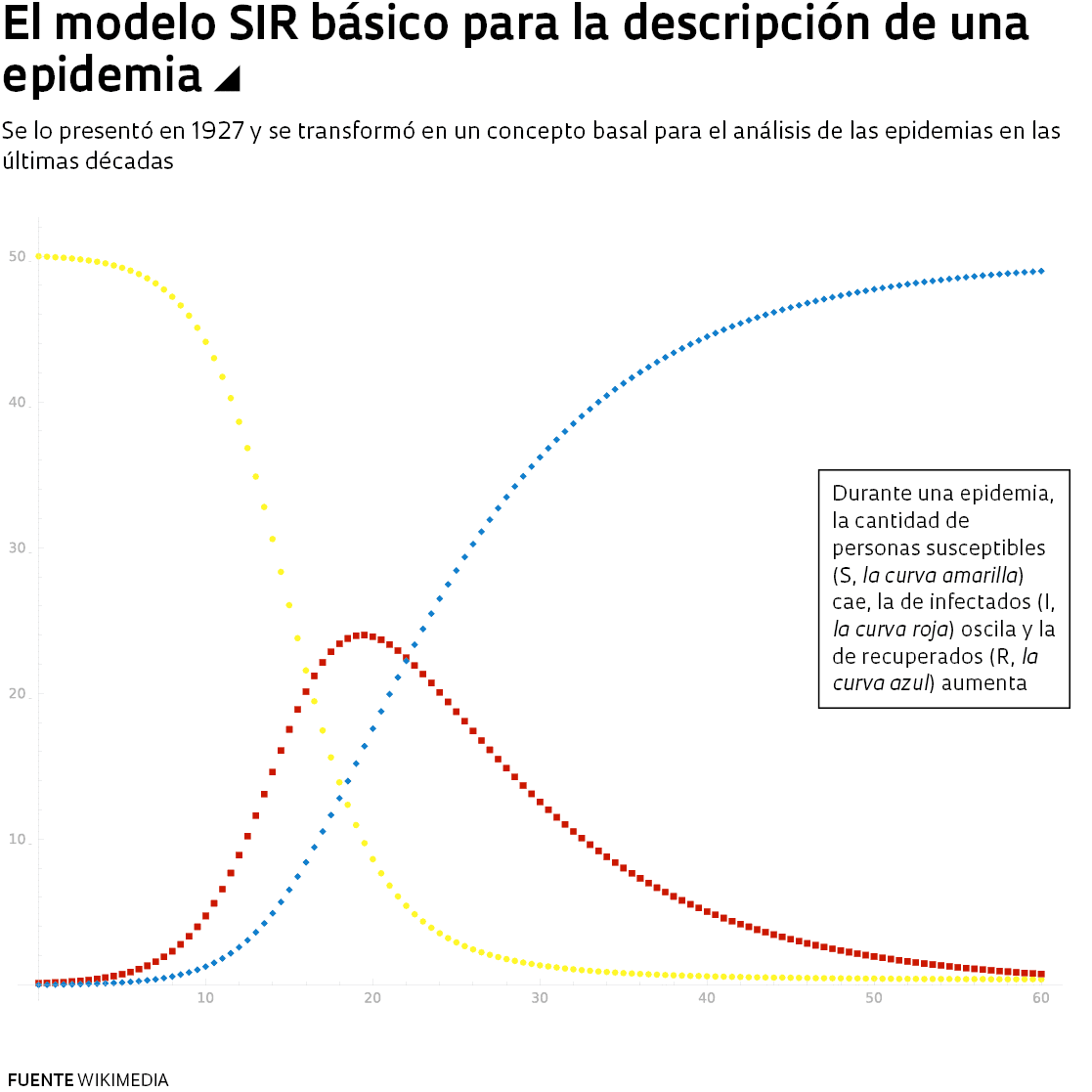
Es difícil acordarse de otra instancia en la que el modelado matemático de las enfermedades infecciosas haya gozado de tanta visibilidad y haya sumado tanto prestigio. “Esta valoración probablemente se debe al desconcierto que generó la pandemia, pues nadie esperaba un panorama tan serio”, comenta el médico epidemiólogo Eduardo Massad, quien asumió el cargo de profesor de matemática aplicada en la Fundación Getulio Vargas (FGV) el año pasado, tras jubilarse en la Facultad de Medicina de la Universidad de São Paulo (FM-USP).
“El modelado matemático nunca fue tan necesario como ahora, frente a una epidemia que avanza con tanta rapidez”, reitera el sanitarista y epidemiólogo Hélio Neves, de la Facultad de Ciencias Médicas del hospital Santa Casa de São Paulo (FCM-SCSP) y coordinador del Comité Técnico-Científico Covid-19 de la Secretaría Municipal de Salud de São Paulo.
Los pronósticos de la cantidad de casos o de muertes, si bien aún exhiben márgenes de incertidumbre, en tanto y en cuanto describen situaciones que mutan con rapidez y de las cuales solamente se poseen datos incompletos, expresan el conocimiento acumulado durante al menos 250 años.
– La realidad de los datos
– Los huéspedes naturales
– Comienzan los testeos en Brasil
– Las dimensiones de la pandemia
– El enigma infantil
– Sergio Machado Rezende: Juntos contra el covid-19
– Lazos en recuperación
– Hay que calcularlo
El matemático y físico holandés Daniel Bernoulli (1700-1782), a quien se le atribuye el primer modelo matemático de propagación de enfermedades infecciosas, elaboró un abordaje que reveló la eficacia de la técnica de inoculación preventiva contra la viruela, por entonces, un problema común en Europa.
En 1760, Bernoulli presentó sus ideas en dos artículos, uno en la revista Mémoires de mathématique et de physique y otro en Mercure de France, valiéndose de parámetros que aún en la actualidad se emplean para analizar la trayectoria de las epidemias.
El estudioso dividió a la población en dos grupos: los susceptibles, cuando aún no están infectados; y los inmunes, quienes ya habían adquirido protección contra una enfermedad después de haberla contraído. Sus ecuaciones tuvieron en cuenta tres variables, que hacían que las personas se desplazaran del primero al segundo grupo. La primera era la tasa de reproducción de la enfermedad o ritmo reproductivo básico, que refleja la transmisión de las personas infectadas a las susceptibles. La segunda era la tasa de mortalidad derivada de la enfermedad. Y la última era la expectativa de vida al momento de la infección. Los cálculos asumieron que el índice de inmunización sería del 100% –la vacunación se realizaba con una aguja bifurcada− y no habría riesgo de transmisión del virus de los inoculados a los susceptibles. La vacunación, según concluyó, podría ampliar la expectativa de vida de 26 años y 7 meses hasta 29 años y 9 meses.
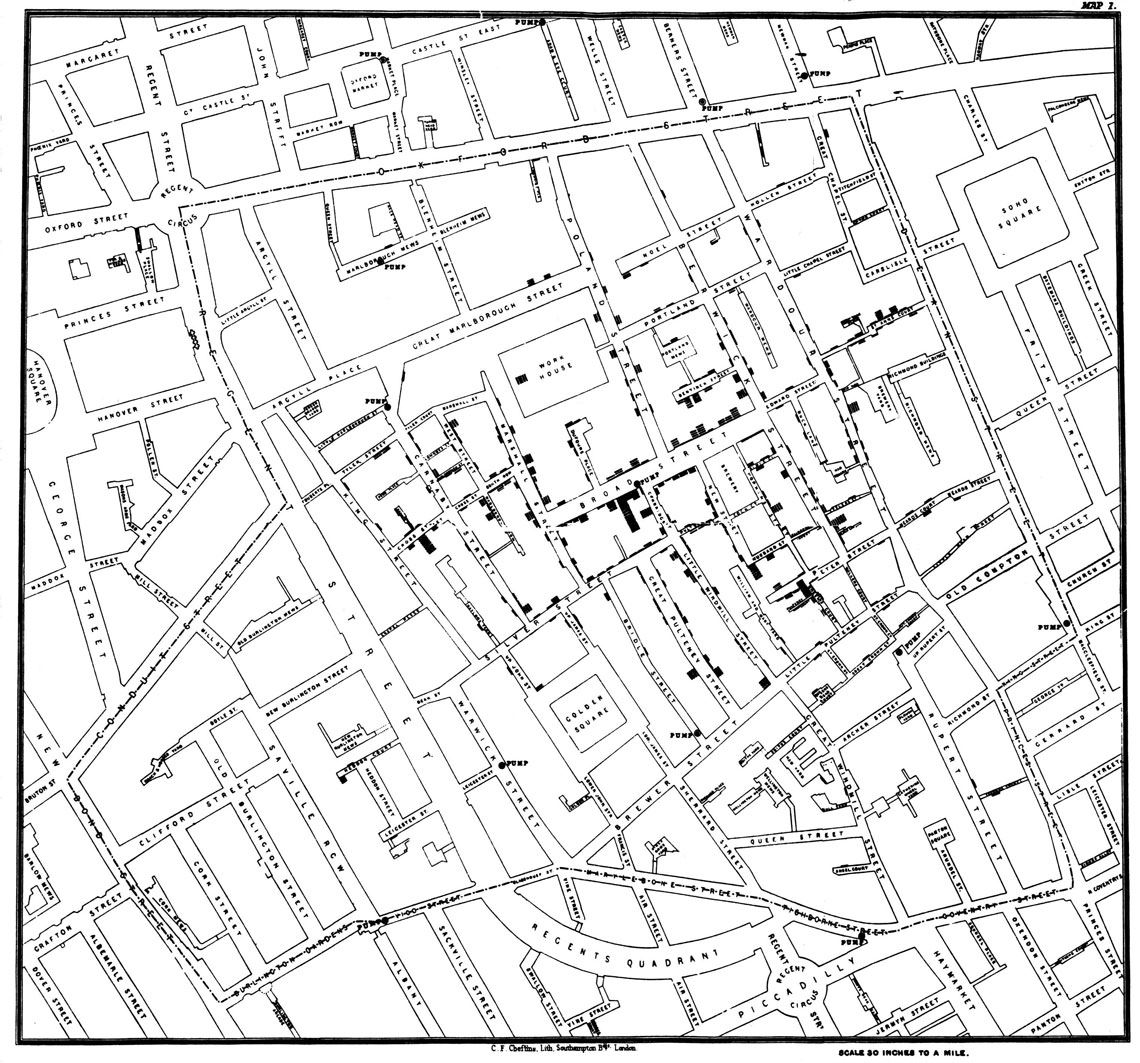
Snow, J. On the Mode of Communication of Cholera, 2nd Ed, John Churchill, New Burlington Street, London, England, 1855/ WIKIMEDIA
Mapa original de John Snow, del barrio de Soho, en Londres, hacia 1854. Los cuadrados y los rectángulos pintados de negro representan las casas de las personas que enfermaron de cóleraSnow, J. On the Mode of Communication of Cholera, 2nd Ed, John Churchill, New Burlington Street, London, England, 1855/ WIKIMEDIAEl cólera en Londres
En 1854, el brote de cólera en Londres que al principio de septiembre de aquel año mató a 127 personas en tan solo tres días, demostró la importancia del trabajo de campo, como complemento de los modelos matemáticos. Incluso sin contar con una formación específica en epidemiología, el anestesiólogo inglés John Snow (1813-1858) determinó que la causa de la enfermedad era el agua contaminada de una bomba de uso público ubicada en Broad Street, en la actualidad Broadwick Street, y no debido al aire pestilente de la ciudad, tal como pensaban sus colegas y las autoridades del gobierno, encolumnados en lo que se denominaba la teoría miasmática.
Snow elaboró un mapa que demostraba que los hogares de aquellos que habían muerto estaban ubicados cerca de la bomba de agua contaminada. El mapa convenció al reverendo Henry Whitehead (1825-1896) de la veracidad de la hipótesis de transmisión del cólera a través del agua y lo apremió para que identificara el primer caso a los efectos de reconstruir la trayectoria del brote, basándose en su conocimiento de los habitantes del barrio de Soho, donde se había iniciado la infección que se expandía. “El reverendo Whitehead fue quien le aportó [a Snow] la evidencia crucial para determinar el verdadero papel que desempeñó la bomba de agua en cuestión”, durante el brote de cólera, relató el lingüista estadounidense Steven Johnson en su libro intitulado The Ghost Map (El mapa fantasma, O mapa fantasma en su edición en portugués de editorial Zahar, 2008].
Cuando contaba con 45 años, Snow murió a causa de un infarto, sin haber ganado reconocimiento por sus ideas. Whitehead estudió otro brote de cólera en Londres, en 1866, en esa ocasión junto al epidemiólogo británico William Farr (1807-1883), uno de los ideólogos de la estadística médica. Con base en las ideas de Snow que él conocía y al formar parte de un comité de salud del gobierno, Farr analizó el agua que dos empresas suministraban a los habitantes de la ciudad. Descubrió que una de ellas distribuía agua contaminada e inmediatamente ordenó que se pusieran carteles de aviso a los residentes para que no consumieran ningún agua que no hubiera sido hervida previamente.
El bioquímico William Ogilvy Kermack (1898-1970) y el epidemiólogo Anderson Gray McKendrick (1876-1943), ambos escoceses, del Royal College of Physicians, de Edimburgo, formularon una teoría sobre la transmisión de las enfermedades infecciosas, que presentaron en un artículo publicado en 1927 en la revista Proceedings of the Royal Society A, que se transformó en la base para los modelos actuales. Ese fue el modelo SIR, correspondiente a las iniciales de los tres grupos, los susceptibles, los infectados y los recuperados, que profundizó los conceptos de Bernoulli. Durante una epidemia, la gente se desplaza de un grupo a otro a medida que un individuo infectado transmite el agente causante de una enfermedad a una comunidad de individuos más o menos susceptibles. La epidemia avanza de acuerdo con las tasas de transmisión y letalidad que varían desde el inicio hasta el final, y se desvanece cuando los susceptibles, tras haber sido contagiados, se tornan inmunes y se recuperan, o en su defecto mueren.
Posteriormente el modelo SIR se perfeccionó. La R pasó a significar removidos, incluyendo, aparte de los recuperados, a los muertos, principalmente a partir de la década de 1970, cuando el modelado matemático comenzó a realizarse por medio de computadoras.
Con base en esos conceptos, a partir de los años 1980 Massad estudió los mecanismos de transmisión del paludismo, el sarampión, el dengue, la fiebre amarilla y, en forma más reciente, el síndrome respiratorio agudo grave (SARS) y el zika, entre otras enfermedades infecciosas y, cuando ello fue posible, propuso nuevas estrategias de prevención. En 1992, a partir de sus cálculos, la Secretaría de Estado de Salud de São Paulo (SES-SP) pudo ahorrar alrededor de 15 millones de dólares al vacunar solamente a los niños entre 1 y 10 años, en lugar de seguir la recomendación de la Organización Panamericana de la Salud (Opas) que estipulaba inmunizar a toda la población comprendida entre los 9 meses y los 15 años con la vacuna triple, que inmuniza contra el sarampión, la papera y la rubeola (lea en Pesquisa FAPESP, edición nº 8). Más tarde, se probó que la estrategia paulista estaba en lo cierto, tal como se describe en un artículo publicado en 1993 en la revista Epidemiology & Infection.
“Utilizamos el modelo SIR, pero con muchas más subdivisiones”, explica el físico Roberto Kraenkel, docente del Instituto de Física teórica de la Universidade Estadual Paulista (IFT-Unifesp). Junto a otros colegas de la USP y de la Universidad Federal del ABC (UFABC), él coordina el Observatorio Covid-19 BR, una plataforma digital creada el 15 de marzo que recopila análisis sobre la evolución del número de casos de la enfermedad en Brasil. “Clasificamos a la población según varias divisiones: susceptibles, expuestos no infecciosos e infecciosos, y estos últimos, a su vez, según su gravedad, leves y graves, y hospitalizados o no. Finalmente, también están los removidos, porque se inmunizaron o porque fallecieron”, comenta.
El equipo del Observatorio está integrado actualmente por 40 científicos de Brasil, de Estados Unidos y de Alemania. “Ellos son sumamente ágiles en su labor”, sostiene Neves, del hospital Santa Casa y de la Secretaría Municipal de Salud, que provee los datos sobre los casos registrados en la capital paulista. “Les planteo un problema, ellos efectúan los cálculos y estimaciones y, en tres horas, ofrecen una respuesta”.
Según él, los pronósticos al respecto de la cantidad de casos y de muertes están siendo útiles para planificar la ampliación de la red de laboratorios de test de diagnóstico y de camas en los hospitales, el uso de escuelas y centros deportivos para cobijar a los pacientes con casos leves de covid-19 y las tareas en los cementerios públicos. “El índice de ocupación de los hospitales municipales no ha sobrepasado el 60%, porque estamos ampliando continuamente la disponibilidad de camas”, dice Neves. “El mayor problema es que no sabemos cuándo será el pico de la epidemia”.
Uno de los grupos del Observatorio determinó cuáles son las ciudades con mayor riesgo de difundir y de recibir el virus desde São Paulo, Río de Janeiro, Minas Gerais, los tres estados de la región sur y los nueve del nordeste, con base en el flujo del tráfico en las carreteras. Los estudios fueron publicados en versión de preimpresión en abril, en la base de artículos científicos SciELO.
“Para la dispersión del virus, es tan importante el tamaño de las ciudades como la cantidad de conexiones o de líneas de ómnibus interurbanas que conectan con otras ciudades”, explica el ecólogo Paulo Guimarães, investigador del Instituto de Biociencias de la USP y coordinador del análisis sobre el estado de São Paulo. Por esa razón, según él, Campinas y São José do Rio Preto presentan alta vulnerabilidad, proporcionalmente mayor que su población, a causa de las conexiones, en el caso de la primera, con otras 214 ciudades, y la segunda, con 135.
“El diálogo entre los expertos de áreas diferentes ha sido muy productivo”, reitera la epidemióloga Maria Amélia Veras, de la FCM-SCSP, que colabora con el Observatorio analizando los datos enviados y las conclusiones. “Los modelos intentan aproximarse a la realidad con parámetros conocidos previamente, en función de enfermedades similares”, subraya. De hecho, un grupo de epidemiólogos de la Fundación Oswaldo Cruz (Fiocruz) se basó en un banco de datos sobre la gripe en Brasil, el Infogripe, para prever la evolución del covid-19 en el país. Otro grupo, de la Universidad de Brasilia, adaptó un modelo matemático utilizado en la epidemia de sarampión para estudiar el alcance de la enfermedad en el Gran São Paulo.
“El límite principal de los modelos es la calidad de la información que los alimenta, porque estamos analizando fenómenos que mutan a gran velocidad”, pondera Veras. Si bien hay evidencias de que el covid-19 es más grave en personas mayores de 60 años, no se conoce la tasa de contagio entre grupos de edades diferentes ni la cifra real de personas infectadas, puesto que solo se testea a los pacientes hospitalizados.
Otro problema coadyuvante en la imprecisión de los resultados radica en que la tasa inicial de transmisión del virus entre individuos (R0), se transforma en tasa reproductiva efectiva (Re) a lo largo de la epidemia. Los valores por encima de 1 indican que el número de casos está aumentando, cerca de 1 reflejan estabilidad, y por debajo, marcan una disminución de casos nuevos.
En la ciudad de São Paulo, hacia el final de abril, el Re oscilaba en torno a 1, lo que significa que un individuo contagiado le transmitía el virus a otro, en promedio. “Estamos atravesando una etapa con una cifra estable de casos, pero todavía es un valor alto, en un rango de 100 a 200 casos graves nuevos por día en el municipio”, dice el ecólogo de la USP Paulo Inácio Prado, uno de los coordinadores del Observatorio Covid-19. “No es una situación confortable, si bien es mejor que el crecimiento exponencial que se registró en la primera quincena de marzo, cuando el Re se ubicaba en valores en torno a 2 y 3”.
Todavía no se conoce la dimensión real de la epidemia en el país, dada la acumulación de test de diagnóstico que aún restan por hacerse. “Este rezago en los análisis genera una subnotificación y provoca que, en los modelos, la epidemia parezca más lenta de lo que en realidad es”, dice Kraenkel.
“Vamos corrigiendo los modelos a medida que aparecen los datos, pero siempre corremos un gran riesgo de incurrir en errores”, dice Massad. Según él, solo podría estimarse el alcance probable de la pandemia luego de que pase al menos un año de su finalización, por medio de lo que se denomina seroprevalencia, la cual indica, mediante análisis hematológicos, el porcentaje de personas con anticuerpos contra el virus en relación con la cantidad de casos registrados de personas infectadas.
Artículos científicos
BERNOULLI, D. Essai d’une nouvelle analyse de la mortalite causee par la petite verole et des avantages de l’inoculation pour la prevenir. Mémoires de mathématique et de physique, presentés à l’Académie Royale des Sciences. n. 1. 1760.
BERNOULLI, D. Reflexions sur les avantages de l’inoculation. Mercure de France, n. 173, 1760.
KERMACK, W. O y MCKENDRICK, A. G. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society A – Mathematical Physical and Engineering Sciences. v. 115, n. 772, p. 700-21. 1º ago. 1927.
MASSAD, E. et al. A model-based design of a vaccination strategy against rubella in a non-immunized community of Sao Paulo State, Brazil. Epidemiology & Infection. v. 112, n. 3, p. 579-94, 1993.
MUNIZ, D. G. et al. Vulnerabilidade das microrregiões do estado de São Paulo à pandemia do novo coronavírus (Sars-CoV-2). Preimpresión Scielo. 15 abr. 2020.
MAIA, K. P. et al. Vulnerability of micro-regions within Northeast Brazil to the new coronavirus (Sars-CoV-2) pandemic. Preimpresión Scielo. 17 abr. 2020.
EMER, C. et al. Vulnerabilidade das microrregiões da região Sul do Brasil à pandemia do novo coronavírus (Sars-CoV-2). Preimpresión Scielo. 23 abr. 2020
ROCHA FILHO, T. M. et al. Expected impact of Covid-19 outbreak in a major metropolitan area in Brazil. medRxiv. Preimpresión. 14 mar. 2020.
Libro
JOHNSON, S. O mapa fantasma – Como a luta de dois homens contra o cólera mudou o destino de nossas metrópoles. Río de Janeiro: Zahar, 2008.